고차원 데이터의 경우 변수의 수가 많다는 의미는 불필요한 변수 존재 + 시각적 표현 어려움 + 계산 복잡도 증가 등의 문제가 발생하낟.
이를 위해 주요 변수만 선택 하는 것을 차원 축소라고 한다.
차원축소 방법
- 변수 선택(Selection): 분석 목적에 부합하는 소수의 예측 변수만을 선택
- 선택한 변수 해석 용이하지만 변수간 상관관계 고려가 어렵다.
- 변수 추출(Extraction): 예측 변수의 변환을 통해 새로운 변수 추출
- 변수간 상관관계를 고려할 수 있지만 추출된 변수의 해석이 어렵다.

4가지 종류
- Supervised Featue Selection: Information gain, LASSO, Stepwise regression... etc
- Superviesd Feature Extraction: Partial least squares(PLS)
- Unsupervised Feature Selection: PCA loading
- Unsupervised Feature Extraction: Principal component analysis(PCA), Auto Encoder... etc
1. PCA 개요
고차원 데이터를 효과적으로 분석하기 위한 기법. 차원축소(주요 변수 추출, 시각화, 군집화, 압축 등)
- PCA는 n개의 관측치와 p개의 변수로 구성된 데이터를 상관관계가 없는 k개의 변수로 구성된 데이터(n개의 관측치)로 요약하는 방식으로, 이때 요약된 변수는 기존 변수의 선형조합으로 생성된다. ( n x p >> n x k )
- 원래 데이터의 분산을 최대한 보존하는 새로운 축을 찾고, 그 축에 데이터를 사영시키는 기법
- 일반적으로 PCA는 전체 분석 과정 중 초기에 사용
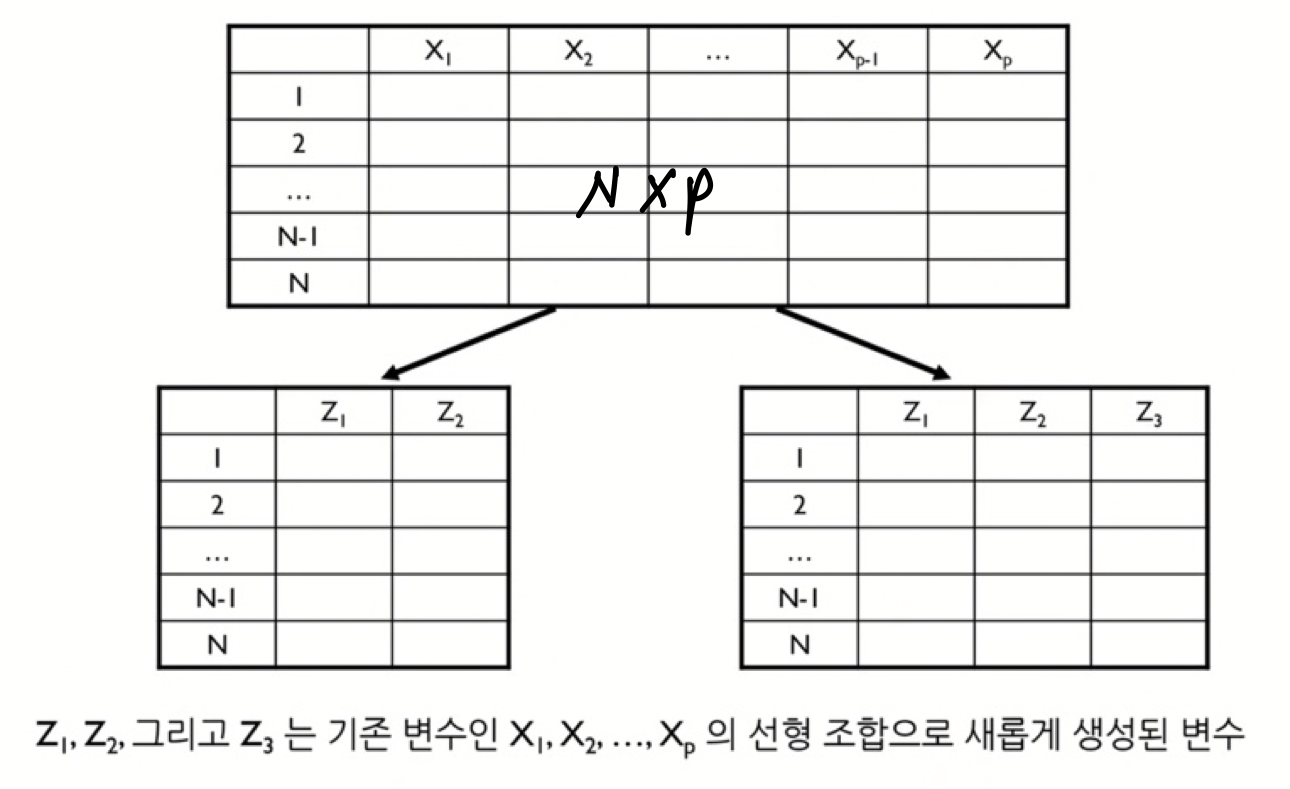
수리적 배경
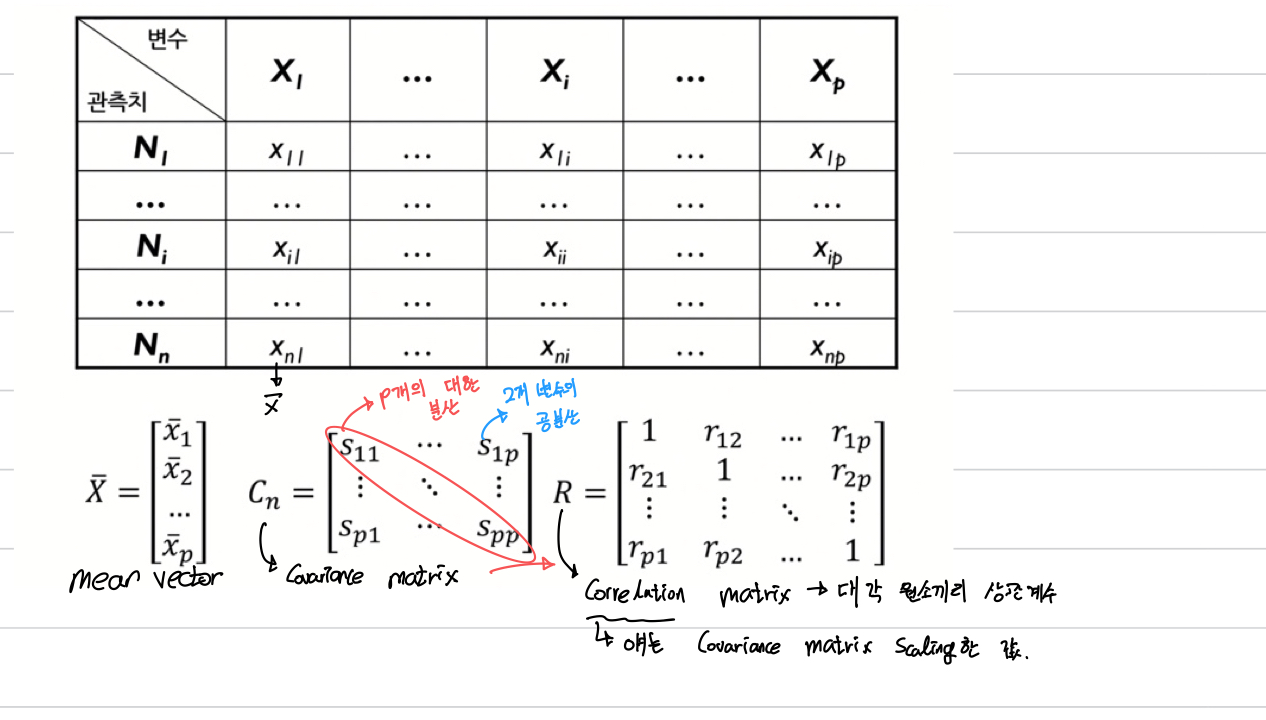


2. PCA 알고리즘




주성분 선택 방식
- 1. 고유값 감소율이 유의하게 낮아지는 Elbow Point에 해당하는 주성분 수 선택
- 2. 일정 수준 이상의 분산비를 보존하는 최소의 주성분 선택(보통 70% 이상)
PCA: X선형결합의 분산을 최대화하는 변수 추출
PLS: X선형결합과 Y간 공분산을 최대화하는 변수 추출
해당 게시물은 고려대학교 산업경영공학부 김성범교수님의 핵심 머신러닝 유튜브를 바탕으로 작성된 글입니다.
