1. 개요
X와 Y의 관계
- 확정적 관계: X로 Y를 100% 설명 가능할 때 ex) F = ma
- 확률적 관계: X와 오차항으로 Y를 설명해야 할 때 ex) 반도체 수율, 포도주 가격
선형 회귀 모델: 출력변수 Y를 X들의 선형결합으로 표현한 모델
- 선형결합: 변수들을 상수배와 더하기, 빼기로만 결합
목적
- X와 Y 사이의 관계를 수치로 설명
- 미래의 반응변수 Y를 예측
2. 모델

B0, B1, B2 등의 Parameter를 찾는 것이 주요 과정이다.
3. 파라미터 추정(최소제곱법)
일차선형회귀 직선에서

비용함수를 최소화 하는 Parameter를 찾아야 한다. 이때 찾는 일련의 Process를 알고리즘(Algorithm)이라고 한다.
비용함수는 다양한 형태가 있고 각각의 형태마다 Parameter를 찾는 방법이 다르다.
여기서의 비용함수는 Convex(전역 최적해 존재) 하다.

알고리즘을 통해 비용함수를 미분한 후 기울기가 0이 되는 B0, B1를 추정할 수 있고 B0 hat, B1 hat이라고 한다.
즉, 전체적인 프로세스는
1. MSE(평균제곱오차) 비용함수
2. 비용함수 최소화하는 값 찾아야 한다.
3. 비용함수를 미분해 0이 되는 Parameters 추정.
이고 이 Process의 이름이 Least Squares Estimation Algorithm이다.
4. 잔차와 확률오차
잔차는 확률오차가 구현된 값이다.


5. 파라미터 추론
점추정

최소제곱법 추정량의 성질(좋은 추정량인지 아닌지 판단하는 법)
By Gauss-Markov Therom: Least square estimator is the Best Linear Unbiased Estimator (BLUE)
BLUE:
1. Unbiased estimator(불편추정량)
2. 다른 불편 추정량보다 작은 분산을 가지고 있을 때.
이 둘을 모두 만족한다.
구간추정

6. 가설검정

7. R2(결정 계수)
R2

결정계수 R2 = SSR/SST로 정의되며 성질은 다음과 같다.

- 사용하고 있는 X가 Y의 분산을 얼마나 줄였는지의 정도
- Y의 평균값을 이용했을 때 대비 X를 사용하므로써 얻는 성능향상 정도
- 사용하고 있는 X변수의 품질
을 의미한다.
ex)
판매원 수 X1, 광고비 X2, 매출액 Y에서
R2 = 0.683의 의미:
- 판매원 수와 광고비 변수에 의해 매출액 변수의 변동성 68.3% 감소
- 매출액의 단순 평균 대비 판매원 수와 광고비를 이용하면 설명력이 68.3% 증가
- 현재 분석에 사용하고 있는 판매원 수와 광고비의 변수 품질 정도가 100점 기준으로 68.3점
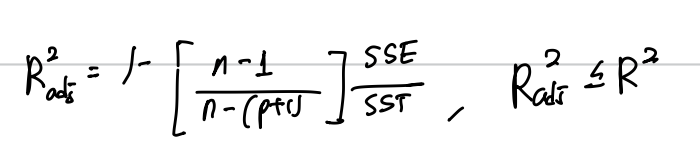
Adjusted R2
- R2는 유의하지 않은 변수가 추가돼도 항상 증가한다.
- Adjusted R2는 R2를 보정해 유의하지 않은 변수가 추가된다면 증가하지 않도록 한다.
- 설명변수가 다른 회귀모형의 설명력을 비교할 때 사용한다.
7. 분산분석(ANOVA)
Analysis of Variance(ANOVA)

SSR와 SSE의 직접적인 분포는 모르지만 모두 카이제곱 분포를 따른다는 것을 알 수 있다.
다음과 같은 방법으로 F분포를 추정해 가설검정을 진행할 수 있다.

해당 내용은 고려대학교 산업경영학과 김성범 교수님의 핵심 머신러닝 유튜브를 바탕으로 작성된 글입니다.