1. 배경
Y가 연속형이 아닌 범주형일 때는 선형회귀와는 다른 방식으로 접근한다.
즉, 새로운 관측치가 왔을 때, 기존 범주 중 하나로 예측(분류 Classification)
선형회귀에서 배운 최소제곱법으로 추정하긴 어렵다.
선형회귀에선 에러가 정규분포를 따르는것과 같은 가정을 따르지 않기 때문이다.

여기서 파이(i)는 베르누이 분포에서 p(성공할 확률)로 생각하면 된다.
2. 로지스틱 회귀분석 알고리즘: Logistic(Sigmoid) 함수

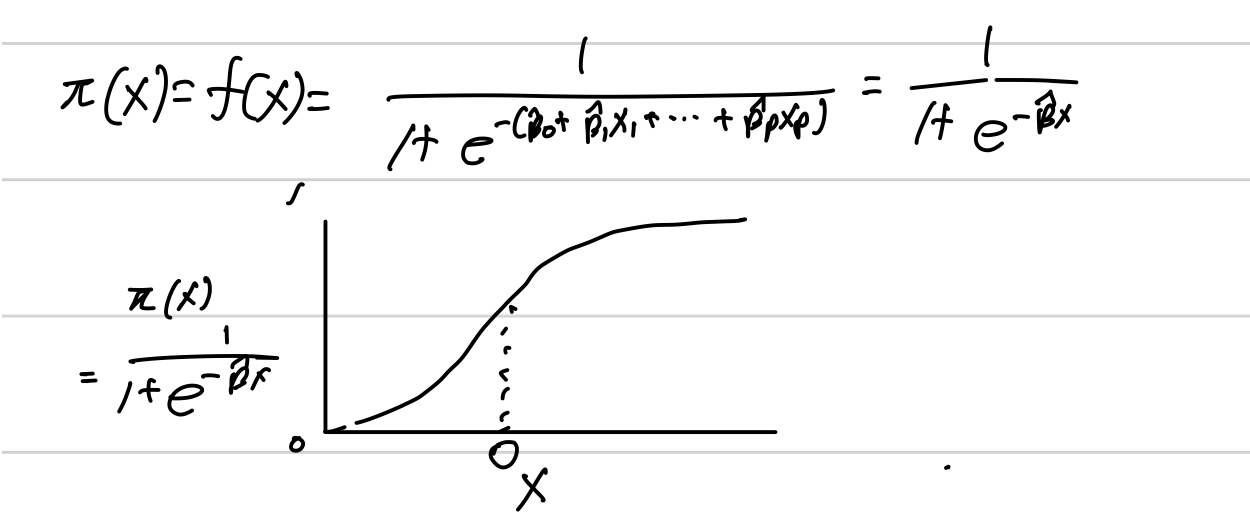
단순 로지스틱 회귀모델: 입력변수 X가 1개인 로지스틱 회귀모델

하지만 여기서 B1의 해석이 중요한데 비선형결합이기 때문에 직관적이지 못하다. B1의 해석을 위해 승산(Odds)를 정의한다.
3. 승산(Odds)
: 성공 확률을 p로 정의할 떄, 실패 대비 성공 확률 비율

즉, Odds: 범주 0에 속할 확률 대비 범주 1에 속할 확률
Odd 적용 후 Log를 취함으로써 Logit Transform(로짓 변환)이 진행되고 이에 따라 단순하게 파라미터를 표현 가능하다.
즉 B1의 의미: X가 한단위 증가 헀을 때 log(odds)의 증가량
4. 파라미터 추정

로지스틱 회귀 모델 학습: by 최대 가능도 추정법(Maximun Likelihood Estimation)
Maximum Likelihood Estimation
가능도(likelihood): 확률밀도함수를 x가 아닌 세타의 함수로 간주하는 것.

- 로그함수는 증가함수이므로 가능도(L세타)를 최대로 하는 세타의 값과 로그가능도를 최대로 하는 세타의 값은 같다.
- 로그가능도는 일반적으로 오목함수이며, 세타에 대해 미분 가능한 함수인 경우가 많다.
- 함수가 오목함수이며 미분가능한 경우는 미분 값이 0인 곳에서 최대가 된다.
- 함수가 오목함수일 충분조건을 두번 미분한 함수의 값이 항상 음수일 때이다.
Logistic Regression에서 파라미터 추정

하지만, Parameter B에 대해 log likelihood function이 비선형이므로 명시적인 해가 가 존재하지 않는다.
그렇기에 수치 최적화 알고리즘을 통해 해를 구한다.

Log-Likelihood 함수가 최대 = Cross Entropy 최소 와 같다. 이떄 수치 최적화 이후 B값을 추정한 후 그래프는 다음과 같다.
- Log Likelihood Function의 최대 = 입력 분포 p(x)와 파라미터가 주어졌을 때, 출력분포 q(x)의 확률을 최대로 한다.
- Cross Entropy의 최소: 입력분포 p(x)와 출력분포 q(x)의 차이를 최소
- Log likelihood function의 최대 = Cross Entropy의 최소
5. 결과 및 해석
승산 비율(Odd Ratio): 나머지 입력변수는 모두 고정시킨 상태에서 한 변수를 1단위 증가시켰을 때 변화하는 Odds의 비율
- X1이 1단위 증가하면 성공에 대한 승산 비율이 e^B1 만큼 변화
- 회귀 계수(B hat) > 0: 성공확률 증가(성공확률 >= 1)
- 회귀계수 <0 : 성공확률 감소(0<= 성공확률 <1)

로지스틱 회귀분석 결과값에서 Input X들에 대해
- Coefficient: 해당 변수가 1 단위 증가할 떄 로그아드의 변화량. 양수이면 성공확률과 양의 상관관계, 음수이면 음의 상관관계
- Std.Error: 신뢰구간 구할 떄 사용
- p-value: 해당 파라미터값이 0인지 가설 검정(H0: B = 0), p값이 작아야 귀무가설 기각.
- Odds: 나머지 입력변수는 모두 고정시킨 상태에서 한 변수를 1단위 증가시켰을 때 변화하는 Odds(성공확률)의 비율
ex) Experience = 1.058: 경험이 1년 더 많으면 대출 확률이 1.058배 증가.
해당 내용은 고려대학교 산업경영학과 김성범 교수님의 핵심 머신러닝 유튜브를 바탕으로 작성된 글입니다.
