6.1 소개
웹의 경쟁적 지형은 지금까지 본 네트워크 모형 중 어떤것도 설명할 수 없다. 에르되시-레니ㅡ모형에서 가장 큰 노드는 전적으로 우연히 결정하고, 바라바시-알버트 모형은 더 현실적인 그림을 제공해 가장 오래된 노드가 언제나 가장 많은 링크를가진다고 한다.
하지만, 현실에서 노드의 성장 속도는 나이에만 의지를 하지 않고 실제 네트워크에서 자주 관찰되는 노드와 링크 삭제, 노드의 나이 듦 같은 실제 네트워크의 동역학과 위상을 예측하기 위한 조정이 필요하다.
6.2 비안코니-바라바시 모형
적합도: 성공적인 노드들은 공통적으로 자신을 무리의 앞으로 나아가게 하는 고유한 특성을 지닌다.
ex)어떤 사람들은 우연한 만남을 오래 지속되는 사회적 관계로 바꾼다.
즉, 적합도는 우연한 만남을 오래 지속되는 우정으로 변화시키는 개인의 재능이다.
바라바시-알버트 모형에서 노드의 성장 속도는 링크수만으로 결정된다고 가정했다. 6.2절에서는 적합도의 역할을 고려하기 위해, 선호적 연결은 노드의 적합도 η와 링크수 k의 곱에 따라 이뤄진다고 가정한다. 이 결과가 비안코니-바라바시 모형 또는 적합도 모형(Fiteness model)이다.
- 성장: 즉, 여기서는 m개링크 + n_j적합도의 노드 j가 추가
- 매 시간 m개의 링크와 적합도 η_j를 가진 새 노드 j가 네트워크에 추가된다. 여기서 적합도 η_j는 적합도 분포(fitness distribution)에서 무작위로 고른 값으로 적합도가 결정되면 바뀌지 않는다.
- 선호적 연결
- 새 노드가 기존 노드 i에 연결될 확률을 다음과 같이 노드 i의 링크수 k_i와 적합도 η_i의 곱에 비례한다.

가장 큰 적합도를 가진 노드가 시간이 흐르면서 가장 큰 허브로 성장한다.
식 6.1에서 π_i가 k_i에 비례하는 것은
- π_i가 k_i에 비례하는 것은 링크수가 높은 노드가 더 잘 보여서 선ㅌ택될 가능성이 높다.
- π_i가 n_i에 비례하는 것은 링크수가 같은 두 노드 중 적합도가 높은 노드가 더 높은 확률로 선택된다.
6.2.1 링크수 동역학
각 노드의 시간에 따른 진화를 예측할 수 있다.
식 6.1에 따라 노드 i의 링크수는 다음과 같은 비율로 변한다.

바라바시 알버트 모형에서 B = 1/2였다.
식 6.4에 따르면 비안코니-바라바시 모형의 동적 지수는 노드의 적합도에 비례하기 때문에, 노드는 자기만의 동적지수를 가진다. 그에 따라 적합도가 높은 노드의 링크수는 더 빨리 늘어난다.
6.2.2 링크수 분포
비안코니-바라바시 모형으로 만든 네트워크의 링크수 분포를 연속체 이론으로 계산하면 다음과 같은 결과가 나타난다.

식 6.6은 링크수 분포가 적합도 분포의 구체적인 형태에 의존한다는 것을 보여준다.
모형의 성질을 설명하기 위해 다음 두 가지 적합도 분포의 설명을 설명하기 위해 식 6.4와 식 6.6을 이용해 동적지수 B(η)와 링크수분포 p_k를 계산한다.
- 똑같은 적합도
- 모든 적합도가 똑같은 경우 비안코니-바라바시 모형은 바라바시-알버트 모형으로 돌아간다.
- 균일한 적합도 분포
- 노드들의 적합도가 각기 다르면 재미있는 결과가 나타난다. η를 구간 [0,1]에서 균일하게 선택한다. 이때 C는 초월방정식의 해로 다음과같이 주어진다.
- 이때 링크수 분포는 링크수 지수가 r = 2.255인 거듭제곱 법칙을 따른다. 다만, 완벽한 거듭제곱 법칙이 되지는 않는다.

정리하면, 비안코니-바라바시 모형은 서로 다른 내재적 성질을 지닌 노드들이 서로 다른 비율로 링크를 얻는다.
이 모형으로 노드 적합도 η가 그 노드의 성장률을 결정한다는 것을 예측할 수 있고, 링크수 분포가 적합도 분포에 어떻게 의존하는지도 알 수 있다.
6.3 적합도 측정
노드의 적합도를 측정해 가시적인 성장을 할 것 같은 노드를 정할 수 있지만, 틀리기 쉽다.
또, 노드의 적합도는 개인이 부여하는 것이 아니라, 그 노드의 상대적 중요성에 대한 네트워크 전체의 집합적 인식을 반영한다.
그렇기에 노드의 적합도는 해당 노드의 시간 변화를 다른 노드의 시간 변화와 비교해 결정할 수 있다.

그렇기에 많은 노드에 대해 링크수의 시간 변화를 추적하면 동적지수 B의 분포는 적합도 분포와 같을 것이다.
비안코니-바라바시 모형의 틀은 각 노드의 적합도 뿐 아니라 적합도 분포의 모양을 결정할 수 있게 해준다. 측정 결과 적합도 분포는 대체로 지수함수적으로 제한되어 있는데 이는 노드들의 적합도 사이의 차이가 작다는 것을 의미한다.
웹의 적합도 분포가 단순한 지수함수를 따르고, 연구논문의 적합도는 정점이 있는 분포를 따른다.
6.4 보스-아인슈타인 응축
네트워크 구조는 적합도 분포의 모양에 어떻게 의존하는가?
적합도 분포의 실제 효과는 어떤 네트워크는 보스-아인슈타인 응축(Bosze-Einstein condensation)을 겪는다는 발견을 한 이후에야 이해할 수 있따.
우선, 비안코니-바라바시 모형과 보스 기체(Bose gas)사이의 형식적 관계를 설정할 것이다.(Mapping)
###
Bose gas:
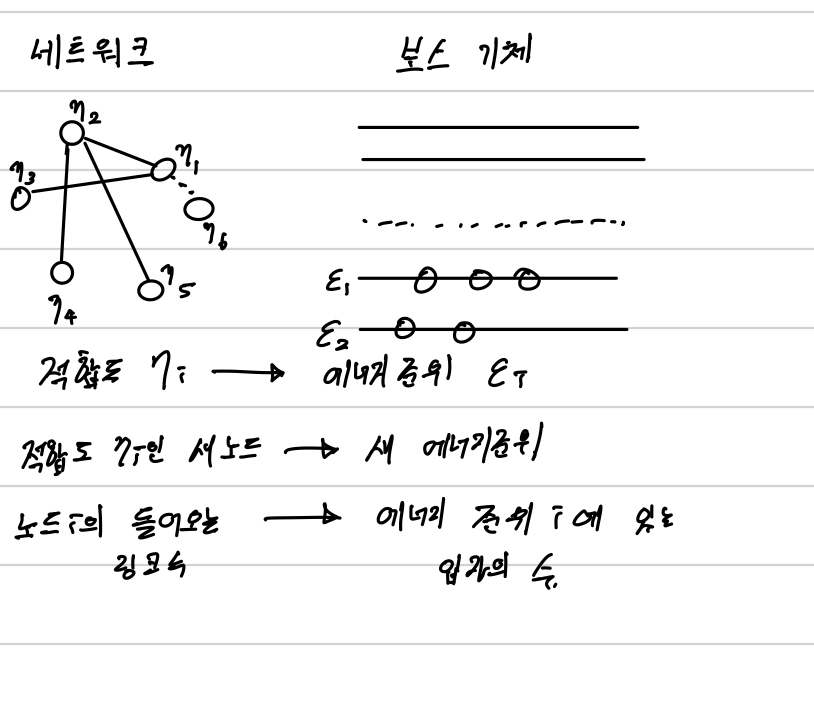
각 노드의 적합도에 에너지 준위 e를 본뜸으로써 무작위 에너지 준위를 가지는 보스 기체를 고려할 수 있다. 새 노드 i에서 기존 노드 j로의 링크는 수준이 e_j인 입자에 해당한다.
###
a) 적합도 >> 에너지
각 노드의 적합도 η_i와 에너지 e_i를 다음 식을 통해 연결한다.

b) 링크 >> 입자
노드 i에서 노드 j로 링크가 생길 때마다 에너지 준위 e_j에 입자를 하나 추가한다.
c) 노드 >> 에너지 준위
m개의 링크를 가진 새 노드가 네트워크에 생길 떄마다 보스 입자에서는 새 에너지 준위 e_j와 m개의 새 입자가 추가된다.
이 입자들의 에너지는 새 노드와 연결된 기존 노드의 에너지 준위로 결정된다.
적합도 모형의 링크는 양자 기체의 아원화 입자처럼 행동한다.
보스 기체로의 본뜨기는 정확하며 2개의 서로 다른 상태의 존재를 예측한다.
6.4.1 척도 없는 상태
대부분의 적합도 분포에 대해 네트워크의 동역학은 '적합하면 부유해진다(fit-gets-rich)'는 원리를 보여준다. 즉, 각 노드의 링크수는 궁극적으로 적합도가 결정한다는 것이다. 가장 적합한 노드가 결국 가장 큰 허브가 되지만 동시에 어느 순간에도 링크수 분포는 거듭제곱을 따른다.
즉, 생성된 네트워크는 scale-free 구조를 가진다.
6.2에서 논의한 균일한 적합도 분포를 가지는 모형은 scale- free 상태가 된다.
6.4.2 보스-아인슈타인 응축
보스 기체로 본뜬 것의 예측하지 못한 결과는 어떤 적합도 분포의 경우에 생기는 보스-아인슈타인 응축의 가능성이다.
보스-아인슈타인 응축 상태에서 모든 입자는 가장 낮은 에너지 준위에 모여서 나머지 에너지 준위는 모두 텅텅 빈다.
네트워크에서 보스-아인슈타인 응축이 가지는 의미는 가장적합한 노드가 링크의 상당수를 차지해 슈퍼허브가 되는 것이고, 그 결과는 scale-free network가 아니라 허브-바큇살 구조로 나타나도, 정성적으로 승자독식 현상(scale-free 없어짐)이 나타난다.
균일분포 같은 적합도 분포는 척도 없는 구조를 만들어내지만, 어떤 적합도 분포는 보스-아인슈타인 응축을 허용한다. 보스-아인슈타인 응축을 허옹하면 1개 또는 몇개의 노드가 링크의 대부분을 차지한다.
6.5 변화하는 네트워크
이 절에서는 바라바시-알버트 모형의 여러 한계를 체계적으로 확장해 실제 네트워크의 연결 구조에 영향을 끼치는 다양한 현상을 잡아내는, 다양한 변화하는 네트워크 모형으로 소개할 것이다.
6.5.1 초기 매력도
바라바시-알버트 모형에서 고립된 노드는 새 링크를 얻을 수 없다. 하지만, 실제 네트워크에서는 고립 노드조차 링크를 얻는다.
연결되지 않은 노드가 링크를 얻도록 하기 위해 선호적 연결 함수에 상수를 추가한다.

K에 0을 대입한 후 실제로 초기 매력도가 존재한다면 다음과 같은 두가지 결과를 가진다.
- 링크수 수 r을 키운다
- r = 3 + A/m
- 즉, 초기 매력도가 링크수지수 r을 증가시켜 네트워크는 균질해지고 허브의 크기가 줄어든다.
- 결국 무작위적 요인을 추가해 선호적 연결의 역할을 약화시킨다.
- 링크수가 많은 노드의 경우 A 무시 가능
- 링크수가 작은 노드의 포화를 일으킨다.
- 아래 해를 바탕으로 초기 매력도는 k<A인 링크수를 가지는 노드의 포화를 일으킨다.
- 링크수가 작은 노드에 새 노드가 연결될 확률을 초기 매력도가 강화시켜 이들을 링크스가 높은 노드로 변모시킨다. k>>A인 경우 링크수 분포는 여전히 거듭제곱 법칙을 따르는데 초기 매력도가 연결 확률에 영향을 주지 않기 떄문.

6.5.2 내부 링크
많은 네트워크에서 새 링크는 새 노드를 통해서만 생기지 않고 이미 있는 노드 사이에서도 생긴다. 예를 들어, 월드와이드웹에서 새 링크의 대부분은 내부 링크(Internal link)이다. 내부 링크는 기존 웹 문서 사이에 새로 추가된 URL이다.

- 이중 선호적 연결(A = 0)
- 바라바시-알버트 모델의 확장을 생각한다. 매 시간 새 노드가 m개의 링크와 함꼐 네트워크에 더해진 후 n개의 내부 링크가 뒤따라 만들어진다.
- 새 링크가 나타날 가능성은 그 링크가 연결할 노드의 링크수에 비례한다.
- r = 2 + (m/m+2n)
- 이떄 r은 2와 3 사이의 값을 가진다. 즉, 이중 선호적 연결은 링크수 지수를 3으로부터 2까지 낮추며 네트워크의 이질성을 증가시키고, 내부 링크는 작은 노드를 희생해 서로 연결된 허브들이 더 커지게 만든다.
- 바라바시-알버트 모델의 확장을 생각한다. 매 시간 새 노드가 m개의 링크와 함꼐 네트워크에 더해진 후 n개의 내부 링크가 뒤따라 만들어진다.
- 무작위 연결(B = 0)
- 이 경우, 내부 링크는 그것이 연결하는 노드의 링크수와 상관없이 만들어진다. 내부 링크는 무작위로 고른 노드 사이를 연결한다.
- 이때, 링크수지숴 r = 3+ 2n/ m 이다.
- 어떤 n,m에 대해서도 r >=3이라는 결과를 얻는다. 즉, 네트워크는 내부 링크가 없을 떄보다 더 균질하다.
- 무작위로 더해진 내부 링크는 무작위 네트워크에서 관찰한 과정을 모사하는데, 이로 인해 링크수가 서로 더 비슷해진다.
- 이 경우, 내부 링크는 그것이 연결하는 노드의 링크수와 상관없이 만들어진다. 내부 링크는 무작위로 고른 노드 사이를 연결한다.
6.5.3 노드 제거
많은 실제 시스템에서 노드와 링크가 사라질 수 있지만, 어떤 네트워크에서는 노드 제거의 효과가 불가능하다.
노드 제거의 효과를 살펴보기 위해 바라바시-알버트 모형에서 매 시간 m개의 링크를 가진 새 노드가 네트워크에 생기고 비율 r로 노드를 하나씩 제거해보자. r에 따라 다음과 같은 세가지 영역을 관찰할 수 있다.
- Scale- Free(r<1)
- 제거된 노드의 비율이 새로 생겨난 노드보다 작아서 네트워크는 계속 성장한다.
- 이떄 링크수분포는 다음과 같은 지수를 가지는 거듭제곱 법칙을 따른다.
- 링크수지수 = 3 + 2r/(1-r)
- 즉, 무작위 노드 제거는 링크수지수를 키워 네트워크를 균일하게 만든다.
- 지수 상태(r = 1)
- 노드 생성과 노드 제거가 같은 비율로 이뤄지고, 노드의 크기는 고정된다.
- 이때 네트워크는 척도 없는 성질을 잃는다.
- 쇠퇴하는 네트워크(r>1)
- 이때 제거된 노드 수 >> 새로 생긴 노드이기에 네트워크는 세퇴한다.
노드 제거가 언제나 무작위는 아니며 제거된 노드의 링크수에 의존할 수 있다.
요약하면 대부분의 네트워크에서 노드는 사라질 수 있지만, 네트워크가 계속 성장하는 한 척도 없는 성질은 유지된다.
